Desmos Series Part 3: Systems of Equations

Introduction 

Single Variable Equation problems are common on the digital SAT, so it’s essential to have a clear strategy for tackling them. These problems require you to solve for a variable by isolating it on one side of the equation. To solve them, you might need to apply techniques such as adding, subtracting, multiplying, dividing, or rearranging terms. But once again, we can use Desmos to get around some of these steps! 

Before diving in, make sure to check out the previous blogs in this series: 

• Desmos Tips & Tricks
• Equivalent Expressions
• Systems of Equations

Two Types of Systems of Equations Problems: 

1. Solve the system of equations: Asks you to find the (x,y) coordinate pair that satisfies both equations
   • “What point (x,y) satisfies the system of equations?”
   • “What is the x-value of the solution to the system of equations?”

2. Number of solutions to the system of equations: Asks you to either: a) find the number of solutions, or b) complete the equations so that they have a specific number of solutions
   • “How many solutions exist for this system of equations?”
   • “For what value of a does this system of equations have infinitely many solutions?”
   • “For some value b, this system of equations has zero solutions. What is b?”
   • “At what value of c do these equations intersect exactly once?”

Important Vocabulary: 

• Solution: Any intersection point between the lines of the system of equations on the xy-plane (note: not x- or y- intercepts) 
• xy-plane: A fancy way to describe the x-y axis the graph is on 
• Constant: A number that doesn’t change 
• Coefficient: A number in front of a variable 
• Infinitely many solutions: they create exactly the same line and overlap completely on Desmos (same slope and same y-intercept) 
• No Solutions: they create parallel lines and they will never intersect (same slope but different y-intercept)

Solve the System of Equations:

1. Type the equations into Desmos
2. Click on the intersection point between the two lines (not the x- or y- intercepts)
3. that point (x,y) is your solution1

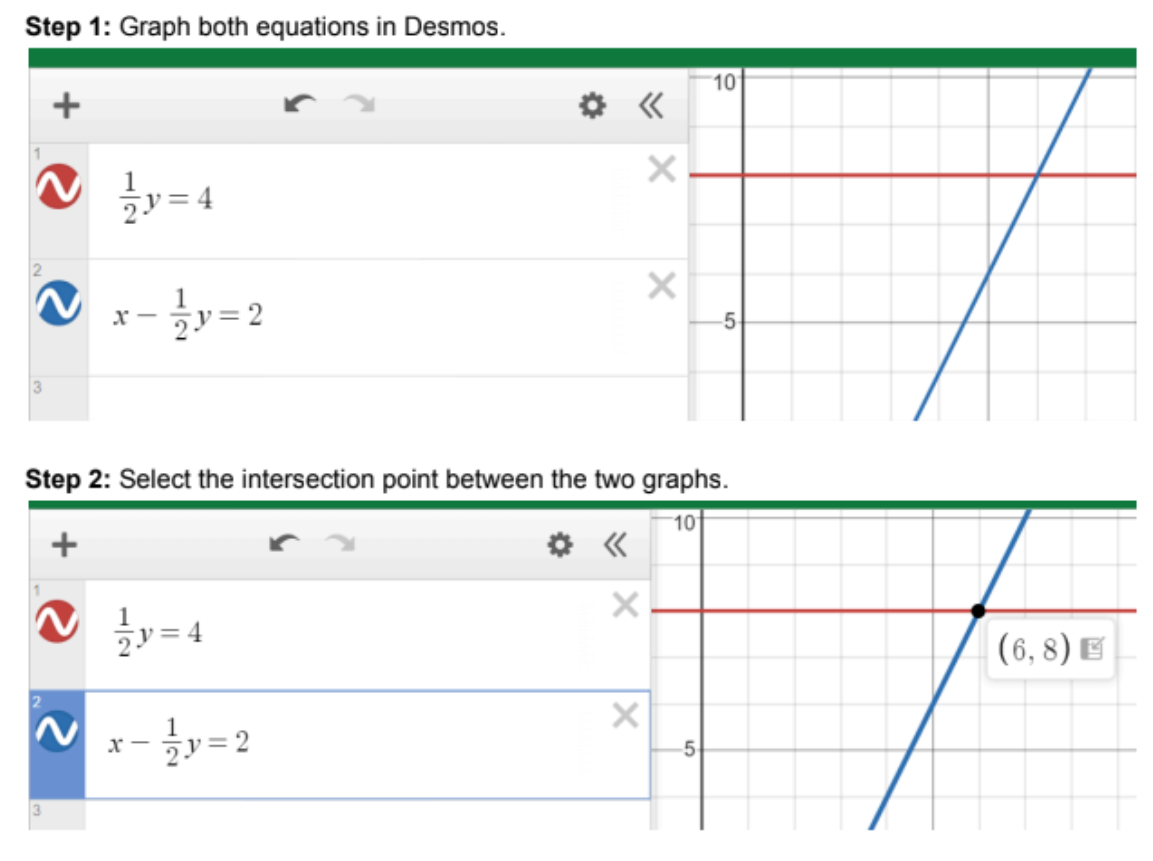
Step 3: Double check what the question is asking. It wants the x-value, so since our (x,y) point is (6,8), the correct answer is D. 6. 

Number of Solutions to Systems of Equations: 

If it asks for the number of solutions or intersections: 

1. Graph the equations 
2. Count the number of intersections between all equations in the system a. If there are 3 equations, an intersection only counts if all 3 lines are intersecting at that point 
3. That number is your answer 

If it asks you to complete the equations so that they have a specific number of solutions:

1. 1. Identify the number of solutions you need to have 
2. Type the equations into Desmos 
3. Create sliders for any variables that aren’t x or y 
4. Slide them around until you have the number of solutions you’re looking for

Tips: 

● Sometimes it helps to isolate y so you have slope-intercept form, then set the slopes and y-intercepts equal to each other to help solve for variables (do this on paper and then plug your solutions back into Desmos to see if those values work!)

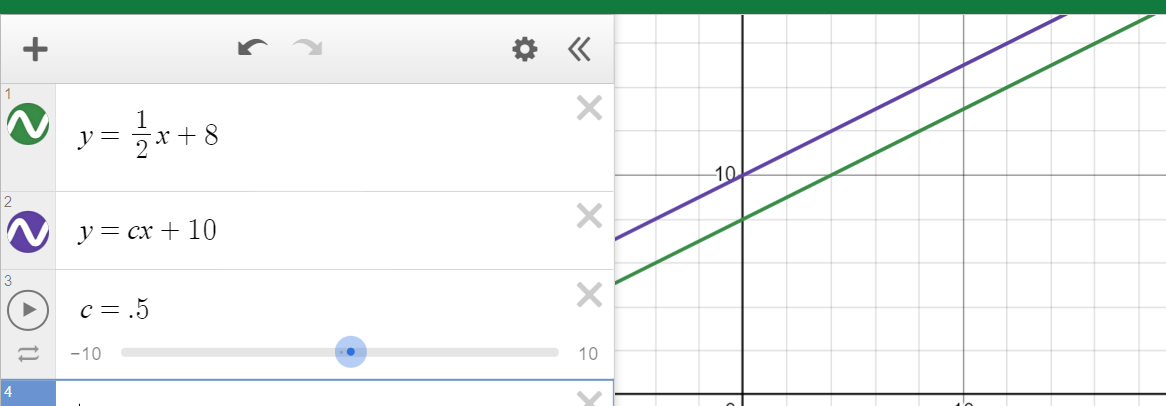
Step 1: Determine the number of solutions we need: it says no solutions, which means the lines should be parallel and never intersect 

Step 2: Type the equations into Desmos. Notice that it can’t graph the second equation because it doesn’t know what c means.

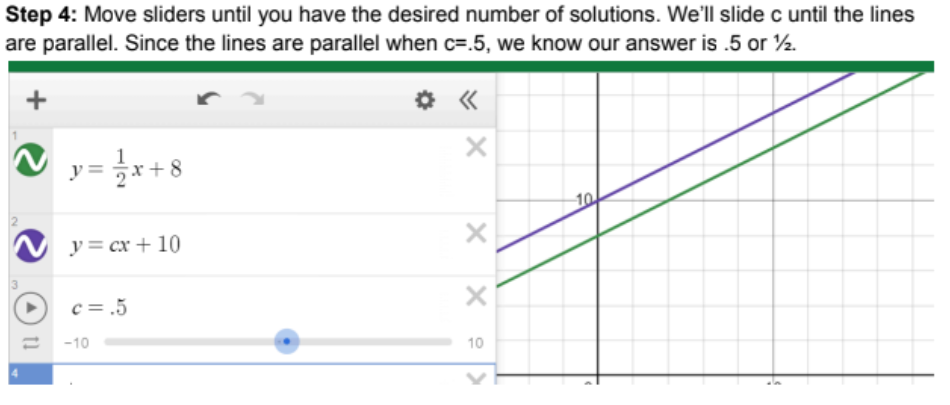
Note: You could also solve this problem by setting the slopes of the two equations equal to each other. We know that to have no solutions, the lines must be parallel, so their slopes must be equal. From the equation y=mx+b, we know that our slope for the first equation is ½, and the slope for the second equation is c. So if we set ½ equal to c, we can see that the lines don’t intersect when c=½ or c=.5. 

Note: If you want to change the range of the slider to be bigger or smaller, just click on the -10 or the 10 at the ends. You’ll be able to change it! 

Now it’s your turn! 

Here are some practice problems for you to try out!

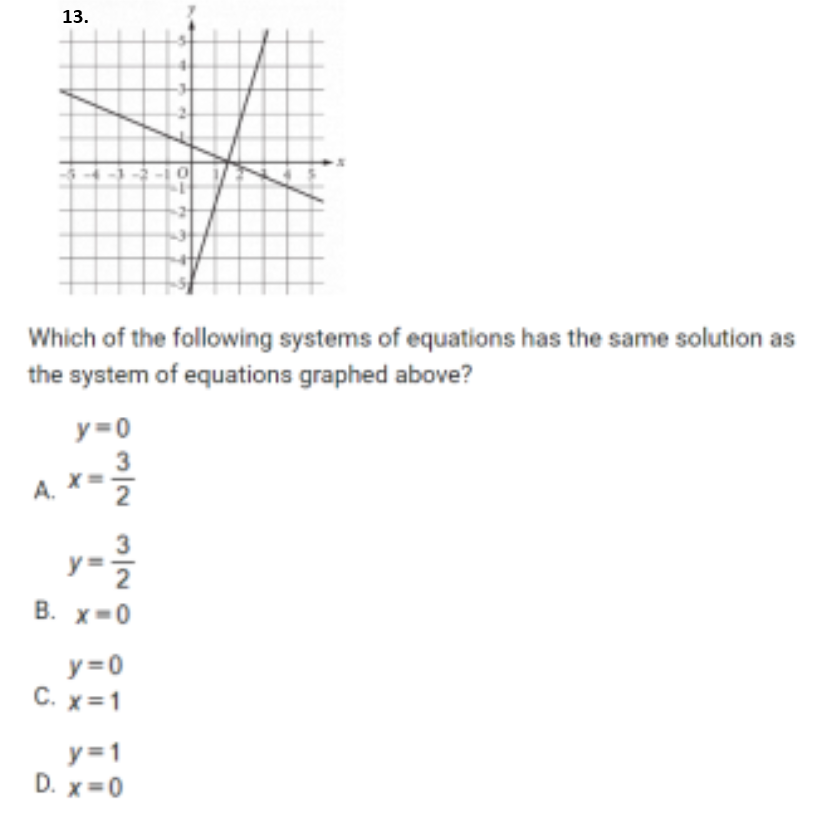
Conclusion 

Practicing these problems using the Desmos trick will help you become more comfortable with identifying single variable equations quickly and accurately. Keep practicing, and you’ll master this skill in no time!