Desmos Series Part 2: Single Variable Equations

Introduction

Single Variable Equation problems are common on the digital SAT, so it’s essential to have a clear strategy for tackling them. These problems require you to solve for a variable by isolating it on one side of the equation. To solve them, you might need to apply techniques such as adding, subtracting, multiplying, dividing, or rearranging terms. But once again, we can use Desmos to get around some of these steps!

Before diving in, make sure to check out the previous blogs in this series, where we covered strategies for tackling Equivalent Expressions problems and general Desmos tips—both of which lay the foundation for mastering Single Variable Equations. Don’t forget, there’s also a helpful trick using Desmos that can simplify your process, reduce errors, and save time!

Single Variable Equation Problems:

These questions ask you to pick the value that, if input to the equation, makes the equation true. 

This may involve adding/subtracting, multiplying dividing, foiling/factoring, or simplifying exponents/logarithms to solve for the variable. However, there is a Desmos Trick for this.

Desmos Trick 1:

1. Type the original expression into Desmos
2. If it doesn’t provide a graph, you may have to sub out the variables for x 
3. A vertical line will appear at the answer (x=). You may have to scroll/zoom to find it.

Tips:

• Make sure to check if the problem is asking for the solution, the sum of the solutions, 3 times the solution, etc.
• If the answer choices aren’t straight forward, graph them as x=[insert answer choice].

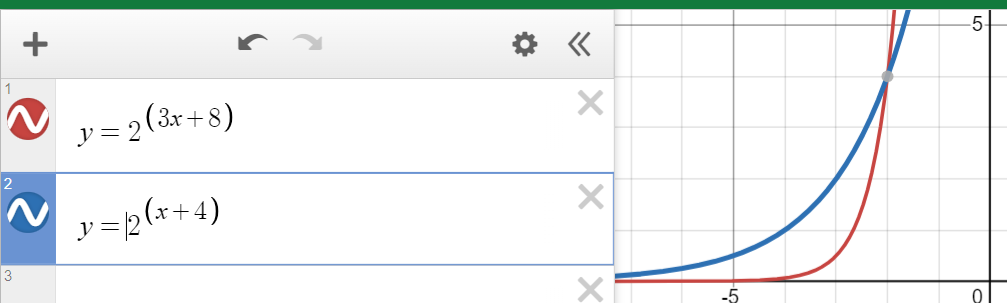
 Example 1:

Which of the following values of a is the solution to the equation above?

1. -2
2. 0
3. 2
4. 4

Step 1: I graphed the equation, replacing a with x. A vertical line appears at x=-2, showing me that the correct answer is A. -2.

Desmos Trick 2:

1. Type both sides of the equation into Desmos set equal to y (“y=…”)
2. If it doesn’t provide a graph, you may have to sub out the variables for x 
3. The x-value of the intersection point will be your solution!

Tips:

• Make sure to check if the problem is asking for the solution, the sum of the solutions, 3 times the solution, etc.
• If the answer choices aren’t straight forward, graph them as x=[insert answer choice].

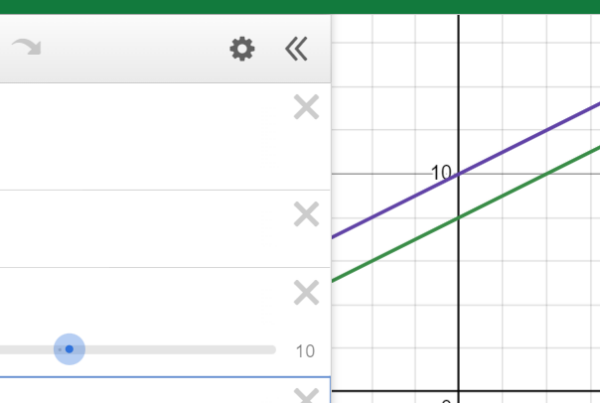
 Example 2: 

We’ll use the same question as Example 1, but we’ll use Strategy 2 this time.

Which of the following values of a is the solution to the equation above?

1. -2
2. 0
3. 2
4. 4

Step 1: I graphed both sides of the equation individually, replacing a with x. A vertical line appears at x=-2, showing me that the correct answer is A. -2.

Step 2: I found the point where the two lines intersect. Since we’re solving for x (or a), we’re going to look at the x-coordinate. The x-coordinate is -2, so our answer is A.

Which trick do I use?

Both of these tricks work well. Ultimately, use the one that makes the most sense to you! If you have trouble using one for a problem, try the other one!

Now it’s your turn! 

Here are some practice problems for you to try out!

1. x(x − 6) + 32 = 3x(x + 2)
What is the sum of the solutions to the equation above?

2. 2 = 2x(x-3) − 2
What is the sum of the solutions to the equation above?
a. 1
b. 2
c. 3
d. 4

3. If 12/x = 300, what is the value of x?
a. 0.04
b. 4
c. 40
d. 80

4. What is the set of all solutions to the equation?
(2x)^(1/2) + 8 = – x
a. -2,4
b. -2
c. 4
d. There are no solutions

5. 5x^2 + 2x = 3x^2 + 10
What is the sum of the solutions to the equation above?

6. x^2 − 5x + 6 = 0
What is the sum of the solutions to the equation above?

7. 4 = 2(x − 1)(x + 2) – 2
What is the sum of the solutions to the equation above?

8. If 3x = 150, what is the value of x?

a. 10
b. 25
c. 50
d. 100

9. What is the set of all solutions to the equation x − 3 = 2x + 1?

a. {−4}
b. {4}
c. {−1}
d. There are no solutions

10. 2x(x + 4) = 4x^2 + 8
What is the sum of the solutions to the equation above?

11. 6x + 3 = 3(2x + 1)
What is the set of all solutions to the equation?
a. {1}\{1\}
b. {0}\{0\}
c. {3}\{3\}
d. There are no solutions

12. If 15x = 600, what is the value of x?

a.20
b. 30
c. 40
d. 50

13. x^2 – 7x + 10
What is the sum of the solutions to the equation above?

14. 5 = (2x + 3)(x − 2) − 15 = (2x + 3)(x – 2) − 1

What is the sum of the solutions to the equation above?

15. What is the set of all solutions to the equation 3x − 9 = 0?

a. {3}\{3\}
b. {−3}\{−3\}
c. {9}\{9\}
d. There are no solutions

Conclusion

Practicing these problems using the Desmos trick will help you become more comfortable with identifying single variable equations quickly and accurately. Keep practicing, and you’ll master this skill in no time!

Answers:

1. -6
2. C
3. A
4. D
5. -1
6. 5
7. −1
8. C. 50
9. A. {−4}
10. −4
11. 2
12. 40
13. 7
14. −1
15. {3}