dSAT Desmos Guide Part 1: Equivalent Expressions

Introduction

Equivalent Expressions problems are common on the digital SAT, so it’s important to have a strategy for how to approach them. These problems ask you to pick an answer choice that is equivalent to a given expression. To solve these questions, you might need to add, subtract, multiply, divide, foil, factor, or simplify exponents and logarithms. However, there’s a helpful trick using Desmos that can decrease the number of overall steps, reduce the complexity, and help us avoid making mistakes!

Equivalent Expressions Problems: Ask you to pick an answer choice that is equivalent to a given expression. 

Expression: any mathematical statement with numbers, variables, and arithmetic symbols in between (no equals signs – that would be an equation)

The goal with these questions is to pick the matching expression. This may involve a lot of arithmetic. However, there is a Desmos Trick to make it easier.

Desmos Trick:

• Type the original expression into Desmos
• If it gives you a graph, type in the answer choices until one of them gives you the same graph
• If it doesn’t, set it equal to an arbitrary number, which will now give a graph. Then, type in the answer choices and set them equal to the same number (if feeling advanced, set it equal to the same constant)
• If the expression doesn’t have x and y, make up numbers!

Example One (just x): 

Equivalent Expressions

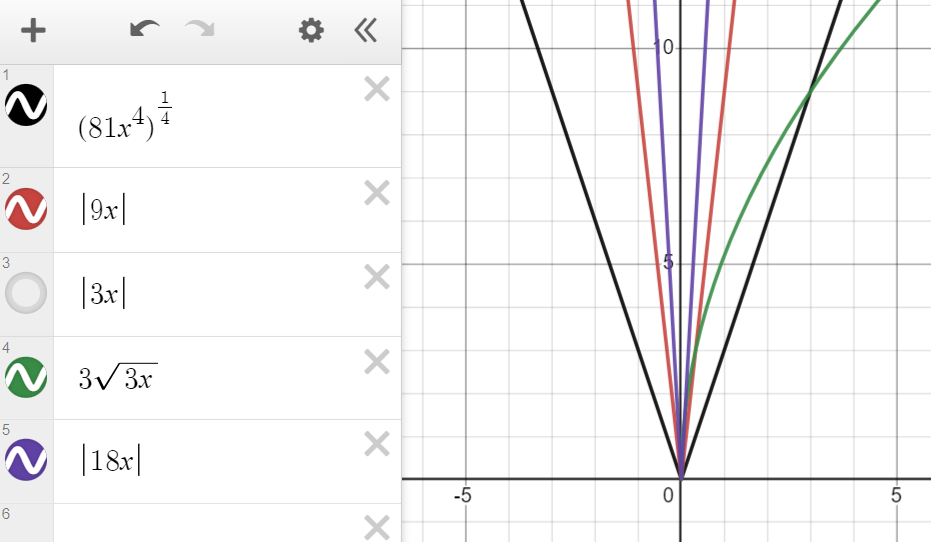
Which of the following expressions is equivalent to (81 x^4)^1/4?

a. |9x|
b.|3x|
c. 3√(3x)
d. |18x|

 Answer choice B is a match because it overlaps the original expression (black). But, we will check the rest anyway:

I turned off answer choice B so that we could see the original expression (black). Answer choices C and D are not matches, so B is the correct answer.

Example Two (x and y):

Equivalent Expressions

Which of the following expressions is equivalent to (64 x^3 y^5)^1/3 , where x>0 and y>0? 

a. 8 xy^(5/3)
b. 4 xy^(5/3)
c. 12 x^3 y^5
d. 16 x^(3/4) y^5

Step 1: Graph the original expression. Unfortunately, this one doesn’t give us a graph. So, I’m going to set it equal to an arbitrary number. I’ll use 2. When I enter the number, I now get a graph. Now, I can start checking the answer choices by setting them equal to the same number.

Step 2: Check answer choices. When I set answer choice A equal to 2, I see that it is close but not a perfect match.

Answer choice B looks like a match! Let’s check the rest.

C and D also don’t look like matches, so the correct answer is B!

Example Three (not x and y):

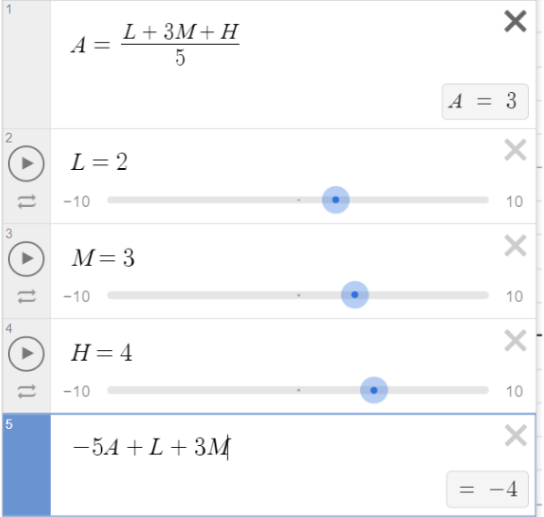
Step 1: Let’s start by typing out the original expression into Desmos and making up some numbers. We’ll set each variable to a different number. This tells us that A = 3. 

Step 2: Now, we’ll type in the answer choices. Since each answer choice says “H = “, we can just type in the second half. When we type out answer choice A, it’s equal to -4. Since H=4, this isn’t our answer. We’re looking for the answer that equals H, which equals 4.

Step 3: Type in the rest of the answers and see which one matches. As we can see, answer choice C is the only one that equals 4. So, C is the correct answer.

Now it’s your turn! 

Here are some practice problems for you to try out!

Conclusion

Practicing these problems using the Desmos trick will help you become more comfortable with identifying equivalent expressions quickly and accurately. Keep practicing, and you’ll master this skill in no time!

Answers:

1. B
2. B
3. B
4. C
5. D
6. A
7. A
8. C
9. C
10. B
11. A
12. A
13. A