On January 30th, 2024, a group of four Dartmouth College professors (from the economics and sociology departments) submitted a report to the college’s president and dean of admissions about the utility of using standardized tests in the admissions process. Not coincidentally, Dartmouth became the first Ivy League institution to reinstate the mandatory submission of standardized test scores as part of the admissions process less than a week later.
Although other colleges had already made the change before Dartmouth, the change at Dartmouth (along with the release of its working group report) seems to have opened the metaphorical floodgates. On February 22nd, Yale joined Dartmouth in implementing this policy change. Brown made the change on March 5th, and Harvard followed suit on April 11th. Outside of the Ivy League, Caltech joined the club on April 11th, and Stanford did the same on June 8th.
What did the Dartmouth working group report on standardized tests actually say? What were their findings? How did the Dartmouth professors reach their conclusions?
Dartmouth Working Group Conclusions
The group of Dartmouth professors drew the overarching conclusion “that the use of SAT and ACT scores is an essential method by which Admissions can identify applicants who will succeed at Dartmouth.” Without quite saying so, they effectively recommended that Dartmouth revoke its test- optional policies and return to a test-mandatory admissions policy. This broad conclusion was supported by four more narrow conclusions:
-
- Standardized test scores are more effective at predicting college success than is high school GPA.
- Standardized test scores are effective at predicting college success for less-advantaged students—not just for more-advantaged students.
- Test-optional admissions policies create unintentional barriers for less-advantaged students.
- Test-optional policies don’t necessarily increase the proportion of applicants from less- advantaged backgrounds.
Dartmouth Working Group Methods
Linear Regression
The working group used relatively straightforward statistical analyses to reach these conclusions. In drawing conclusions #1 and #2, the professors used linear regression to predict students’ first-year college GPAs at Dartmouth. They found that both high school GPA and standardized test scores can be used to predict first-year college GPA. When they used high school GPA alone to predict first-year college GPA, they were only able to explain 9% of the variation in first-year college GPA (R2 = 0.090), while standardized test scores alone were able to explain about 22% of the variation in first-year college GPA (R2 = 0.222). Thus, standardized test scores were able to explain more than twice as much of the variation in college success as high school GPA was able to.
When high school GPA and standardized test scores were used simultaneously to predict first-year college GPA, they were able to explain about 26% of the variation in first-year college GPA (R2 = 0.255). The simplest conclusion here is that it is more effective to use both as predictors than to use either of them separately. That alone should not be terribly surprising. The more interesting finding is that the marginal contribution of standardized test scores is much larger than that of high school GPA. By adding standardized test scores, they were able to explain almost three times as much variance as they could with high school GPA alone (26% vs 9%). Conversely, the marginal contribution of adding high school GPA to standardized test scores was much smaller: an increase of only about 3% (22.2% to 25.5%). Thus, standardized test scores made a much larger contribution to the admissions office’s ability to predict which students were likely to succeed than high school GPA scores did.
Using the results for the model that incorporated both standardized test scores and high school GPA, we could write the equation of the line to predict a student’s first-year college GPA as follows:
predicted college GPA = 0.304 + (0.00139)(SAT Score) + (0.322)(HS GPA)
It might be tempting to see the “weight” or “slope” on high school GPA (0.322) as being higher than that for standardized test scores (0.00139) and interpret this as meaning that high school GPA is actually more important. However, this logic would only work if the two measurements were on the same scale as each other. We know that high school GPA and SAT scores are not on the same scale at all, though, so this technique will not work.
Instead, let’s look at an example. Let’s take an imaginary student with a high school GPA of 3.7 and an SAT score of 1400. This student’s predicted first-year GPA at Dartmouth would be
0.304 + (0.00139)(1400) + (0.322)(3.7) ≈ 3.44. Then let’s think about what would happen if this student could increase his or her GPA by 0.25 points (unlikely, but maybe possible): the new predicted college GPA would be roughly 3.52. Instead of changing the high school GPA, let’s instead put it back at 3.7 and increase the SAT score by 100 points; now the predicted first-year GPA at Dartmouth would be about 3.58. Thus, we can see that changes in standardized test scores seem to have relatively bigger impacts on predicted college GPA.
It is worth noting that this result is almost assuredly not just due to random chance. The regression equation above shows an estimated slope/coefficient for SAT scores of 0.00139, with an associated standard error of 0.0000488. If the true coefficient (or “slope” or “weight” or “predictive effect”) of SAT/ACT scores on first-year college GPA at Dartmouth was actually zero, a result like this would occur less often than once in every 999 trillion occurrences…and I’m only stopping at trillions because most people don’t know what comes after trillions. In other words, there is effectively no possible way that this result could have occurred if the true effect were zero—the ability for SAT/ACT scores to predict first-year GPA at Dartmouth (above and beyond the predictive ability of high school GPA) is not due to random chance. There is a very real relationship between SAT/ACT scores and first-year college GPA, even after accounting for the predictive effect of high school GPA.
This effect is similar for both the more-advantaged group of students and the less- advantaged group of students. We can see this in the figure below (which is pulled directly from the Dartmouth report), where the y-axis represents first-year college GPA and the x-axis represents SAT scores (students who took the ACT had their scores converted to the SAT equivalent). The slopes of the regression lines for the more-advantaged students (navy color) and the less-advantaged students (yellow color) are nearly identical.

The Dartmouth report also cites previous research showing that SAT and ACT scores are predictive of future career success, future earnings, and future graduate school attendance, even after controlling for family income. They also cite a task force report from the University of California system that found similar results: standardized test scores are more effective predictors of college success than high school GPA is. Interestingly, the University of California report also found that the predictive ability of high school GPA has decreased over time due to grade inflation and other changes in high school grading policies. Thus, in the academic community, the Dartmouth report is not particularly groundbreaking—we already knew a lot of this information. What is different this time is that decision-makers are actually listening: unlike the University of California system, which ignored its own research and switched to a test-blind admissions policy, Dartmouth appears to be heeding the advice of the working group report by switching back to a test-mandatory policy.
Descriptive Statistics
Even more straightforward, from a statistical perspective, were the methods used to draw
conclusions #3 and #4. In these cases, basic descriptive statistics (histograms, percentages, etc.) were enough to conclude that test-optional policies may not be having their intended effects. For example, the authors compared distributions of SAT composite scores for different time periods— one when Dartmouth had a test-mandatory admissions policy (Class of 2017-2018) and one when it had a test-optional admissions policy (Class of 2021-2022). These can be seen in the figure below (which is pulled directly from the Dartmouth report). The blue-ish purple color is the test-mandatory class and the pink color is the test-optional class.
One way to interpret this graphic is that the blue-ish purple color represents the full score
distribution for students applying to Dartmouth, while the pink color represents the subset of
scores that are submitted to Dartmouth under a test-optional policy.

Unsurprisingly, we can see that the bulk of the unreported scores seems to come from the lower end of the score distribution. Those with higher scores are reporting them at nearly the same rates under both admissions policies, but lower scores get reported less frequently under a test-optional policy. This then gives the admissions department two options: A. knowing this, they could assume that any student who does not report a score would have been on the lower end of the distribution, or B. they could ignore this effect and admit people who probably would not have actually had good enough scores to get accepted if they had reported their scores.
Both of these options are problematic. If they choose option A, they are potentially punishing disadvantaged applicants who truly (logistically or financially) found it more difficult to take a standardized test or who did not understand the system well enough to know whether they should submit their scores. In fact, the authors of the report found some evidence that this was indeed occurring: they found that less-advantaged and first-generation college students were less likely to report their scores, particularly in the 1450-1550 score range, which likely would have been high enough to significantly help those disadvantaged applicants. See the figures from the report below, where the y-axis is the estimated proportion submitting their scores and the x-axis is the estimated SAT Composite score (or ACT equivalent).
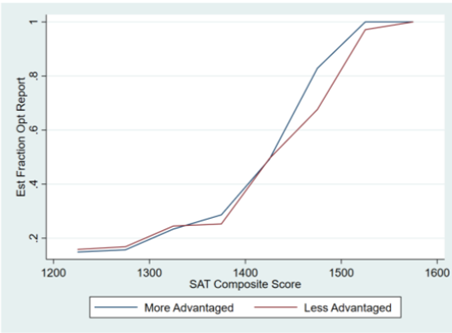
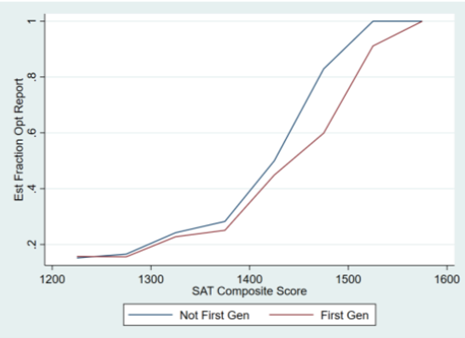
Option B, on the other hand, would mean admitting applicants who would not have been admitted had they actually submitted their scores. This would mean taking spots away from candidates who did submit their scores and who otherwise would have been accepted. This is probably the less problematic of the two options, but it would still mean admitting a class of students who is less well prepared and less likely to succeed in college and in their future careers, which is inherently the opposite of the mission with which college admissions offices are typically tasked.
The report also shows that standardized test scores often benefit—rather than harm— disadvantaged students, at least at Dartmouth. For example, see the figure below from the report. It shows that, at any given SAT score level, less-advantaged students have a higher probability of being accepted; at some score levels, the less-advantaged students have more than twice as high a probability of being accepted as the more-advantaged students do.

Unintentional Barriers of Test-Optional Policies
The large movements over the last few years towards test-optional or test-blind policies have occurred for two reasons. First, the COVID-19 pandemic made it logistically difficult to take standardized tests, so colleges found it difficult or unfair to require them. Second, concerns about the fairness and equity of standardized tests have arisen. These concerns are based on the (generally accurate) view that disadvantaged populations tend to score lower on standardized tests and the (generally less accurate) conclusion that colleges and universities therefore are less likely to admit them because of their lower scores.
The idea, then, was that test-optional and test-blind admissions policies would allow disadvantaged students to remove this bias against them and therefore have better opportunities for college admission. Unfortunately, though, these policies may have unintentionally had the opposite effect. The authors of the Dartmouth report came to this conclusion, as did researchers at Yale. There are three reasons for this. First, without SAT or ACT scores, admissions departments are forced to weigh other components of the application more heavily (guidance counselor recommendations, essays, etc.) which have been shown to favor more privileged students. Second, admissions departments typically have less information about the high schools attended by disadvantaged students, meaning that there is more uncertainty about their academic qualifications. Third, disadvantaged students might be less informed about the admissions process and therefore might elect not to submit their test scores even though these test scores would have improved the students’ chances of admission.
“In Context” and “Whole Person” Application Review Processes
The biggest confusion and misconception in the national media narrative surrounding standardized tests is that colleges and universities treat them as a single measure of whether a student should be accepted or not. As the Dartmouth data show, this is typically not the case in reality. Most colleges use the scores as one piece of information among many pieces of information, and they typically use this information “in context.” This means that a 1400 from one student is not equivalent to a 1400 from another student in an entirely different setting. Based on interviews with admissions officers, the Dartmouth report states this explicitly: “Dartmouth Admissions uses SAT scores within context; a score of 1400 for an applicant from a high school in a lower-income community with lower school-wide test scores is a more significant achievement than a score of 1400 for an applicant from a high school in a higher-income community with higher school-wide test scores.”
When Yale announced that they were following Dartmouth’s lead in returning to a test-mandatory policy, they used a similar argument. They said that “our applicants are not their scores, and our selection process is not an exercise in sorting students by their performance on standardized exams. Test scores provide one consistent and reliable bit of data among the countless other indicators, factors, and contextual considerations we incorporate into our thoughtful whole-person review process.” As with Dartmouth, Yale’s internal research shows that SAT and ACT scores are the best predictor of future success in college.
The changes in policy by Dartmouth and other institutions are good examples of statistical evidence guiding policy decisions. Academic studies have shown consistently that SAT and ACT scores are the best predictors of college success. Importantly, returning to test-mandatory admissions policies is not only helpful for admissions departments, but it is potentially beneficial for less-advantaged applicants. The Dartmouth report is one of the rare cases in which the general public gets to see the data and thought processes that are going into such decisions.
Interested in learning more about Test Prep at Mindfish?
Contact us today to find out what our dedicated tutors can help you achieve.





