For students gearing up to take the SAT or ACT, mastering the art of efficient problem-solving is key to success. One invaluable tool in your arsenal is the TI-Series graphing calculator, equipped with a plethora of functions accessible under the MATH key. In this blog post, we will delve into how students can harness the power of these functions to streamline their problem-solving process and boost their scores on these standardized tests. Sit back and relax, folks: your calculator is about to do a LOT more work FOR you.
The MATH Key
The MATH key on your TI-Series graphing calculator contains a treasure trove of mathematical functions designed to simplify complex calculations. By navigating through these menus, you can access various tools that can save time and help approach problems more strategically.
MATH Menu
From the MATH menu, you can convert any decimal to a fraction using the Frac command. This is an easy way to relate your calculator’s default decimal answers to potential fractions given as multiple choice options. To learn more about your calculator’s default settings and how to manipulate them to your advantage, check out Part 3 of the Calculator Mastery Series. The Frac command is also a useful way to test whether a number is rational: if a number is rational, it can be converted to a fraction.
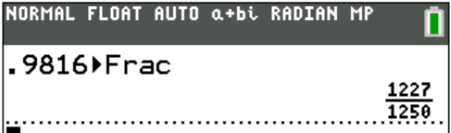
If you’ve changed your calculator’s settings to report answers as fractions (see Part 3 of the Calculator Mastery Series to learn how), you can use the Dec command to convert fractions to decimals. Additionally, the calculator will cube numbers or do cube or Xth roots for you from the MATH menu using the third, fourth, and fifth options, respectively.
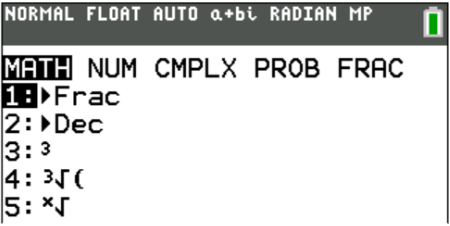
If you’re working with a logarithm with a base other than 10 or e, the LOGBASE function allows you to input that base of the function instead. This cuts down the time and effort needed to evaluate a logarithm by hand:
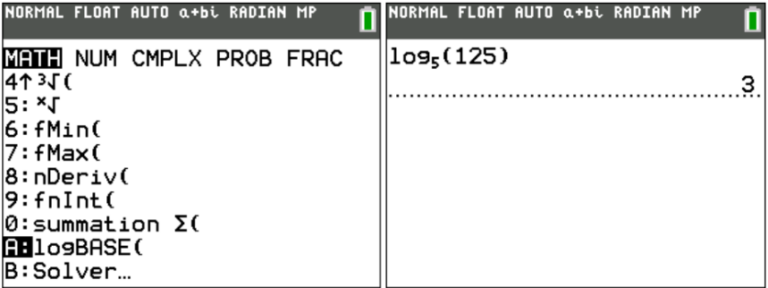
Probably the most unknown, underrated use for a graphing calculator will LITERALLY solve algebraic equations for you! Start by selecting the Solver function, input both sides of the equation, hit the GRAPH button (with the OK over it) to continue, and press ALPHA→ENTER to solve. For proof of concept, I’ll use the calculator to solve an equation whose answer we can readily predict:
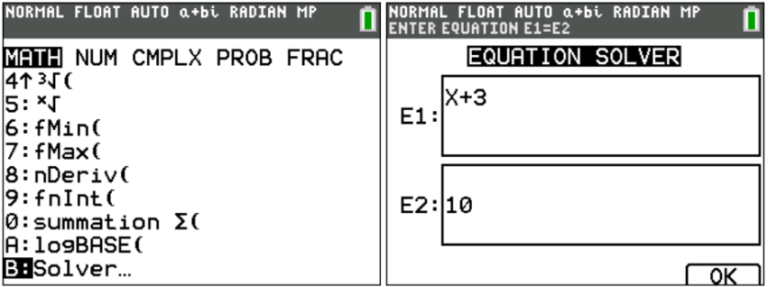
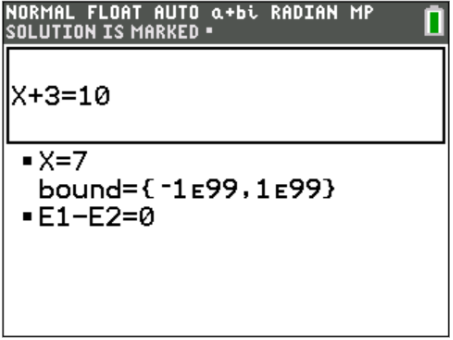
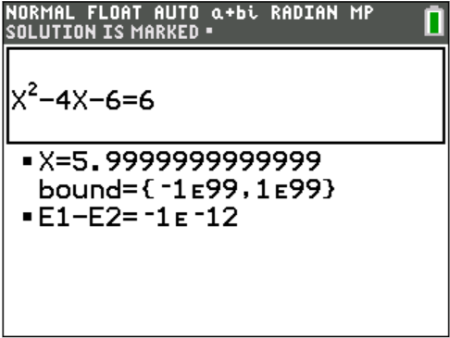
Be careful with higher order equations, though: the Solver function will only give one answer. In the following example, we should also get a solution of x = -2. Don’t worry about the repeating decimal answer either: because the calculator inputs values into the equation until the equation is true, sometimes rounding errors occur. This is the calculator essentially saying that x = 6.
A Calculus Side Note
If you’re in AP Calculus and you’re not acutely familiar with the nDeriv operation by Thanksgiving or the fnInt operation by spring break, I would strongly recommend looking into how to use them. There will be questions on the AP exam that require you to use these operations to differentiate or integrate functions. If you need a hand, feel free to reach out to Mindfish for more guidance.
NUM Menu
There are a few time-saving tools under this menu as well. For example, your calculator will evaluate absolute values using the abs command:
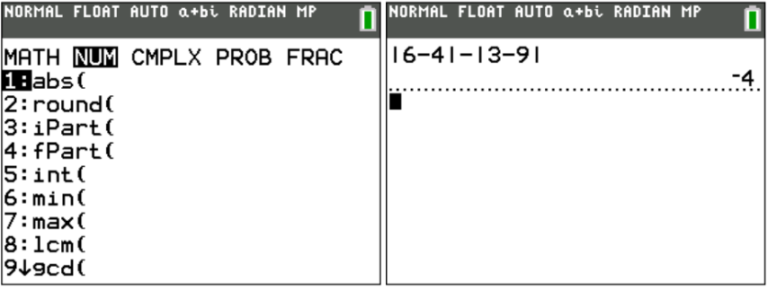
You can also calculate the least common multiple or greatest common factor/divisor of two numbers using the lcm and gcd commands, respectively, making sure to put a comma between the two numbers in question. Unfortunately, you can only calculate the least common multiple or greatest common factor of two numbers at a time.

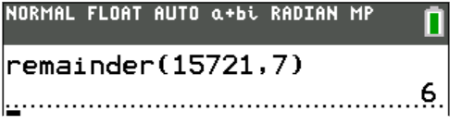
Forgot how to do long division to find a whole number remainder (or just don’t feel like doing the long division in the first place)? No worries! The remainder function will do that for you, too! In this example, I’ve asked the calculator to find the remainder when 15721 is divided by 7:
Scientific Notation
I’ve seen students use several methods for entering numbers in scientific notation into a calculator, and some of them are more prone to errors in order of operation than others. Fortunately, your graphing calculator includes a foolproof way to enter these values, and it’s the most efficient way to work with numbers in scientific notation, too. Simply replace the “times ten to the” part of the number in scientific notation with “EE” (2nd→Comma):

All three of these operations are equivalent, but the first is five keystrokes, the second is six, and the third is seven. (Quick sidenote: I have no idea why the command is “EE” on the calculator, but it types it as one E. The keystrokes in this example would be “7→2nd→Comma (EE)→5→ENTER.” You don’t need to input “2nd→Comma (EE)” twice.)
Complex and Imaginary Numbers
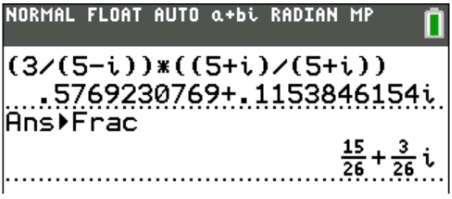
This one is probably my favorite: your calculator has an input for the imaginary number i. It’s the second function of the decimal point key. As I sit writing this post, I can’t help but chuckle about how many of my former students have exclaimed, “Why didn’t my math teacher show me this?!” I can understand why those teachers didn’t mention this shortcut, but it’s there, and it works: all I have to do is copy the expression in this question and hit ENTER. I then used the same Frac operation from earlier to convert this complex answer into a fraction:
Conclusion
It’s fun to poke around the graphing calculator and learn all that it can do, but in the high-pressure environment of standardized tests like the SAT and ACT, every second counts. The functions and operations found within the MATH key on your TI-Series graphing calculator are powerful tools that can give you a significant advantage. By mastering the various functions under the MATH key, you can approach problems more efficiently, saving time and increasing your chances of success on test day. Don’t overlook this invaluable resource – make sure to familiarize yourself with the MATH key functions and incorporate them into your test-taking strategy.




